目录
- 环形队列的插入、删除原理
- BST(二叉查找树)
- 遍历二叉树
- 哈夫曼树
- 大/小顶堆
- 存储序列
- 左孩子右兄弟树与森林
- 快速排序
- 归并排序
- 堆排序
- 闭哈希、开哈希
- 2-3树
- 深度优先与广度优先
- 最短路径长度与最小代价生成树
- 拓扑排序
环形队列的插入、删除原理
环形队列可以用数组(大小等于n)实现,包含front(起始位置)和rear(结束位置),通常只能存储n-1项,以区分空(front==(rear+1)%n)和满(front==(rear+2)%n)的状态。
插入
先判断队列是否已满,如果还没满,rear=(rear+1)%n
删除
先判断队列是否为空,如果不为空,front=(front+1)%n
BST(二叉查找树)
BST上节点的左孩子的值总是小于该结点,右孩子的值总是大于该结点。
遍历二叉树
先序遍历( Preorder traversal )
第一次访问根结点,然后总是先访问左子树后访问右子树(等左子树访问完,而不是访问了左孩子马上访问右孩子)
中序遍历( Inorder traversal )
先访问左子树,再访问树根,再访问右子树。需要注意的是,一定要递归地找到“最左的”左子树再访问。中序遍历是从叶子结点或叶子结点的父节点(当叶子结点的父节点没有左孩子时)开始的。
后序遍历( Postorder traversal )
先访问左子树,再访问右子树,最后访问树根。这一个过程也是递归的,因此第一次访问的结点应该是叶子结点。这个过程也可以说成是,孩子结点被访问了之后才能访问父亲结点。
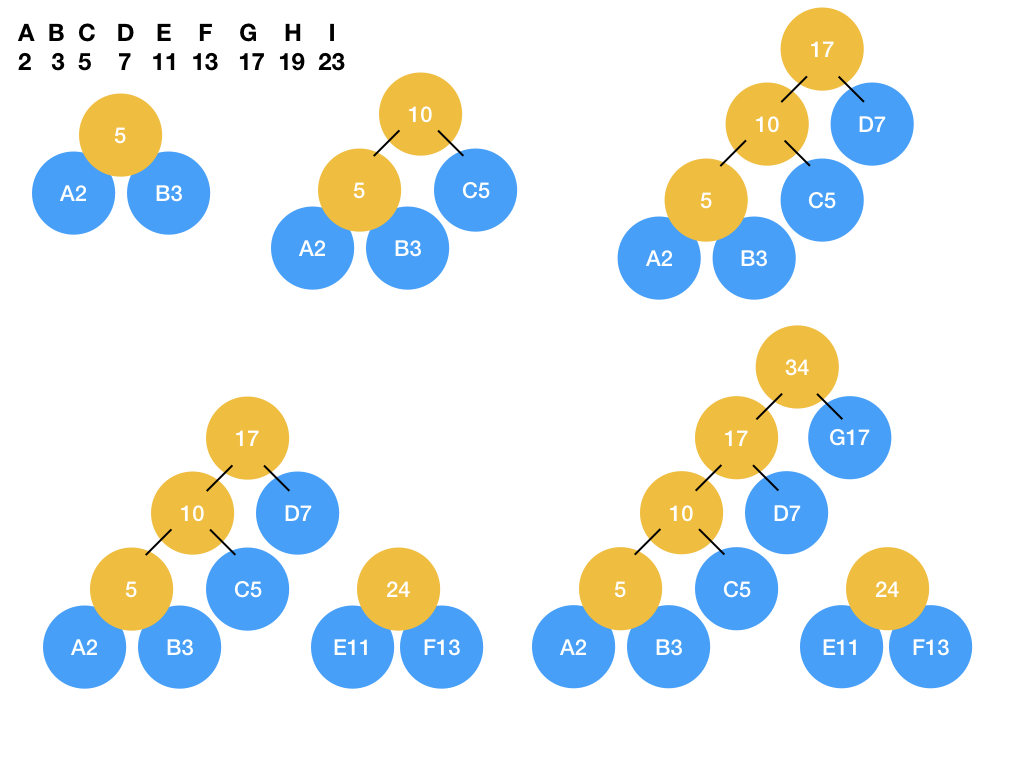
哈夫曼树( Huffman Tree )
哈夫曼编码:一种可变长的编码,具有高频数据项(这里是高频字符)对应编码较短的特点。
哈夫曼树:一种满二叉树,以每个字符作为叶子结点,字符的频率作为叶子的权重。可以据此推断出字符对应的哈夫曼编码。
构建步骤
- 将字符与出现频率对应起来,并由小到大排序,如:A 10 B 20 C 30 D 40
- 选择最小的两个字符结点,它们的父结点的值等于这两个字符的频率(权重)之和。
- 在剩余字符结点与哈夫曼树的树根结点间选择最小的两个结点,将两个结点合成一颗树(此时有多棵哈夫曼树)或将一个结点加入哈夫曼树(这个结点和树根有同一个父节点)。
- 重复第三步直到所有结点被加入哈夫曼树。
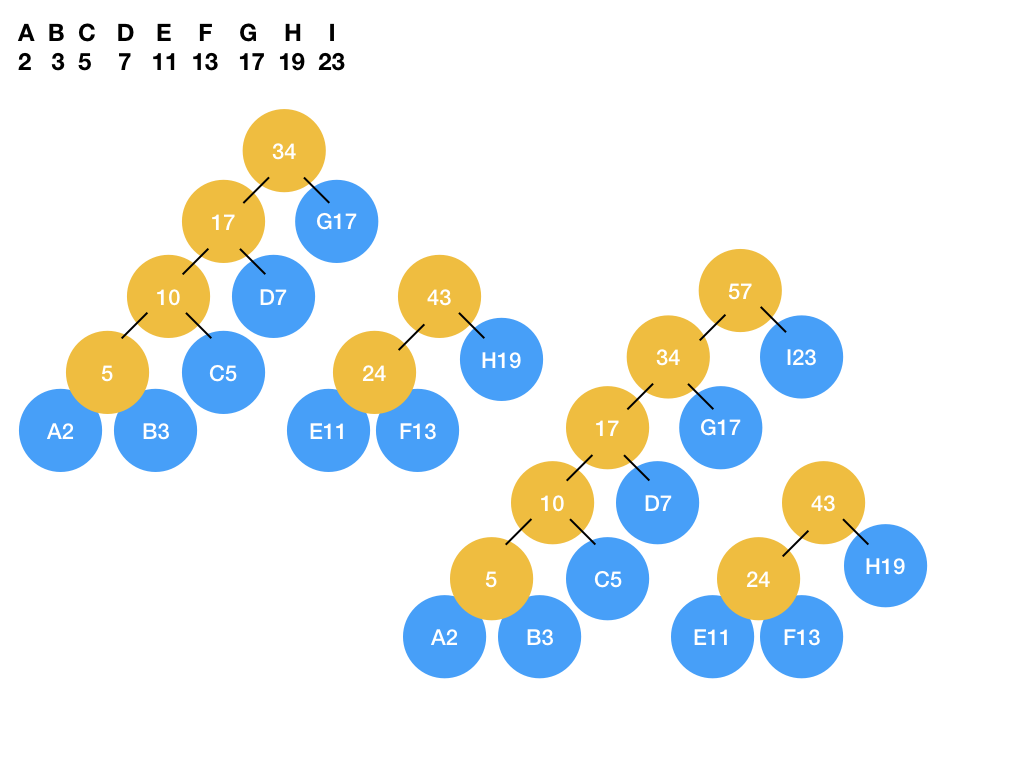
大/小顶堆
小顶堆(Min-heap):树中每个结点的值小于等于孩子节点的值
大顶堆(Max-heap):树中每个结点的值大于等于孩子节点的值
大/小顶堆是一颗完全二叉树(n个结点与满二叉树包含的n个结点对应,连续存储在数组中),并且父亲结点总是大于/小于孩子节点的值。
插入
新的结点插入到堆的尾部,如果父亲结点与新结点的关系不满足堆的约定,交换新结点与父亲结点的位置。
给出一组数( 10,5,12,3,2,1,8,7,9,4 )要求依次插入大顶堆
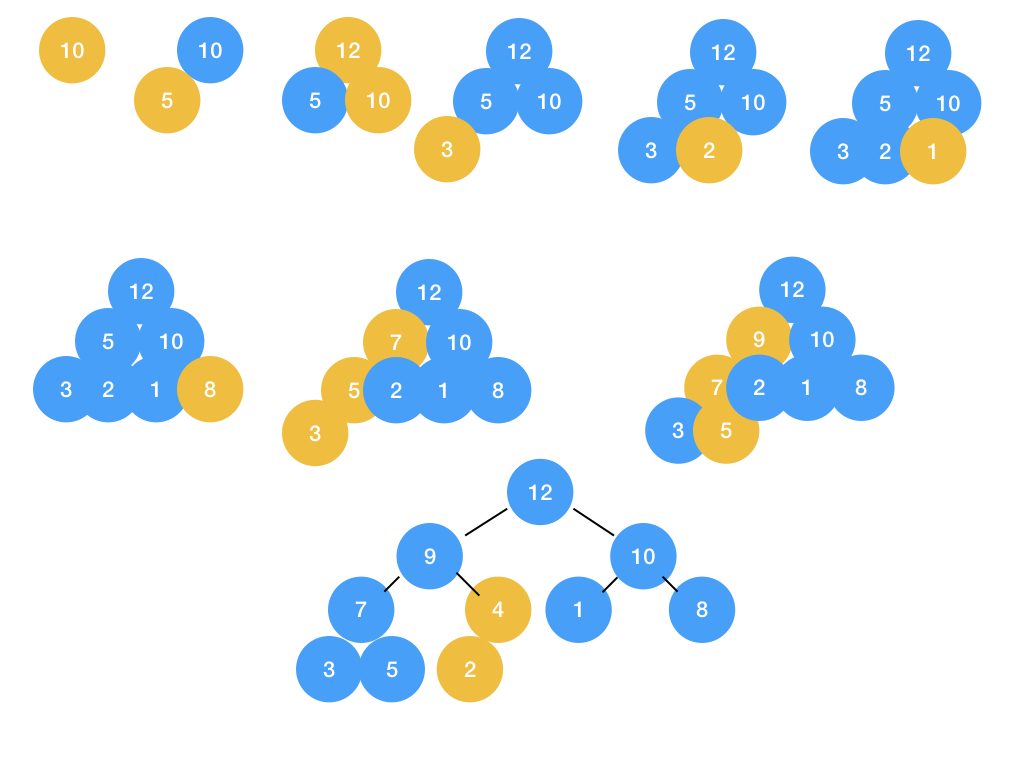
删除
将堆尾部的元素与将要删除的元素交换位置,再重新调整先前处于尾部的元素的位置。
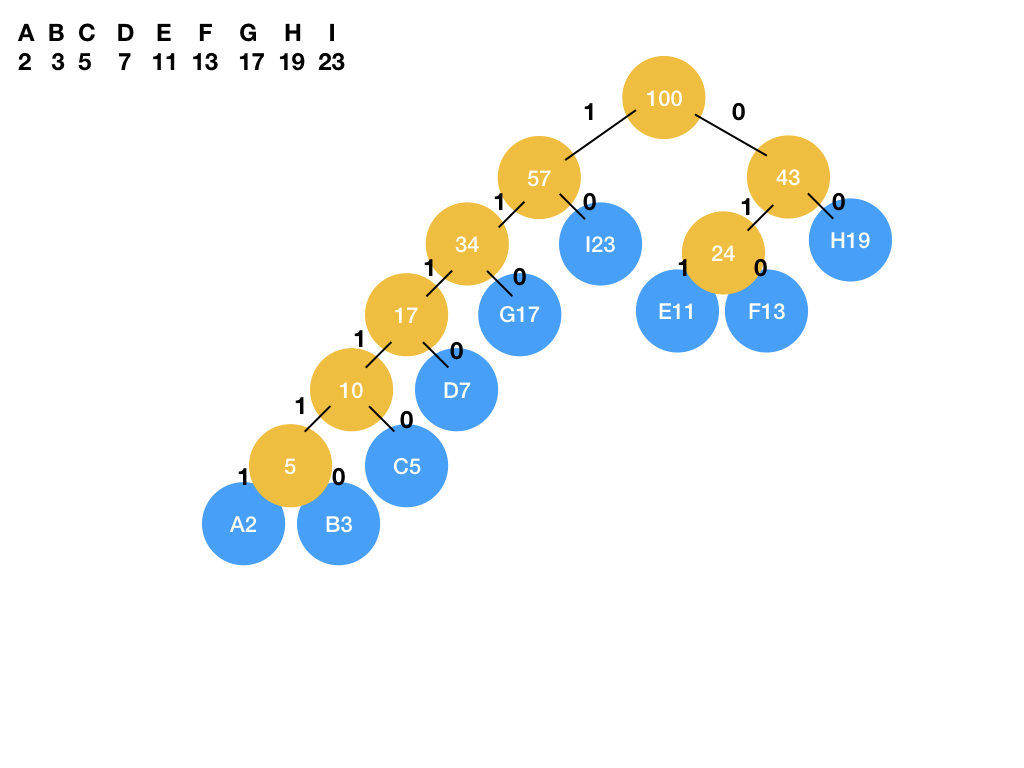
存储序列
存储序列可以存储任何类型的树,它包括结点的值/关键字和右括号,如”XPC)Q)RV)M))))”,右括号表示它前面的结点已经是叶子结点。存储序列与存储树的数组顺序相同,但存储序列去掉了不必要的空值,也是先序遍历的访问顺序。
示例
给定存储序列 XPC)Q)RV)M)))) ,还原树的结构

左孩子右兄弟树与森林
左孩子右兄弟树是一种二叉树,但任意类型的树都可以转化为左孩子右兄弟树,由于树根也可以有兄弟结点,这时我们可以将多棵树组合成一片森林。
快速排序
理论最快的排序算法,一般情况下的复杂度为nlogn,详细介绍见《快速排序算法(C++)介绍和简易实现》。
归并排序
和快速排序的复杂度相同,并且无论数据如何分布,复杂度都能保持在nlogn,但一般情况下和快速排序有小于一个数量级的差异。
归并排序递归地将一组数据分为两个部分,直至分成只有一个数的最小单元,然后最小单元两两合并,合并后的单元继续合并,直至恢复原来的长度。
合并(Merge)的过程是,两个指针指向两个数组最左侧(最小的数),比较指针指的数的大小,将较小的数放入temp数组中,然后向右移动指向较小数的指针,继续比较,当一个指针指向了最右的数,另一个指针之后的数都可以放入temp。
针对合并的过程,也可以再组织一个数组,前半部分正向存储数组,后半部分反向存储,同样拥有两个指针,形如:1367|5432。这么做的好处是不需要判断指针是否越界,两个指针指向同一位置时合并过程结束。
堆排序
前面复习过大顶堆和小顶堆,对堆来说,取最大值/最小值的复杂度Theta=1,但调整堆的复杂度是logn,因此利用不断取堆的最大值排序,复杂度Theta=nlogn。
建堆的复杂度是n,看起来有点反直觉,但一般情况下,越是高层的结点越少被调换,详细解释可以参考知乎《堆排序中建堆过程时间复杂度O(n)怎么来的?》。
闭哈希、开哈希
哈希表通过哈希函数与关键字推断数据位置或插入数据,不可避免地出现重合。闭哈希与开哈希的不同在于它们解决冲突的策略——闭哈希将数据插入后面的位置,开哈希用链表的方式扩展冲突项。
闭哈希( Closed Hashing )
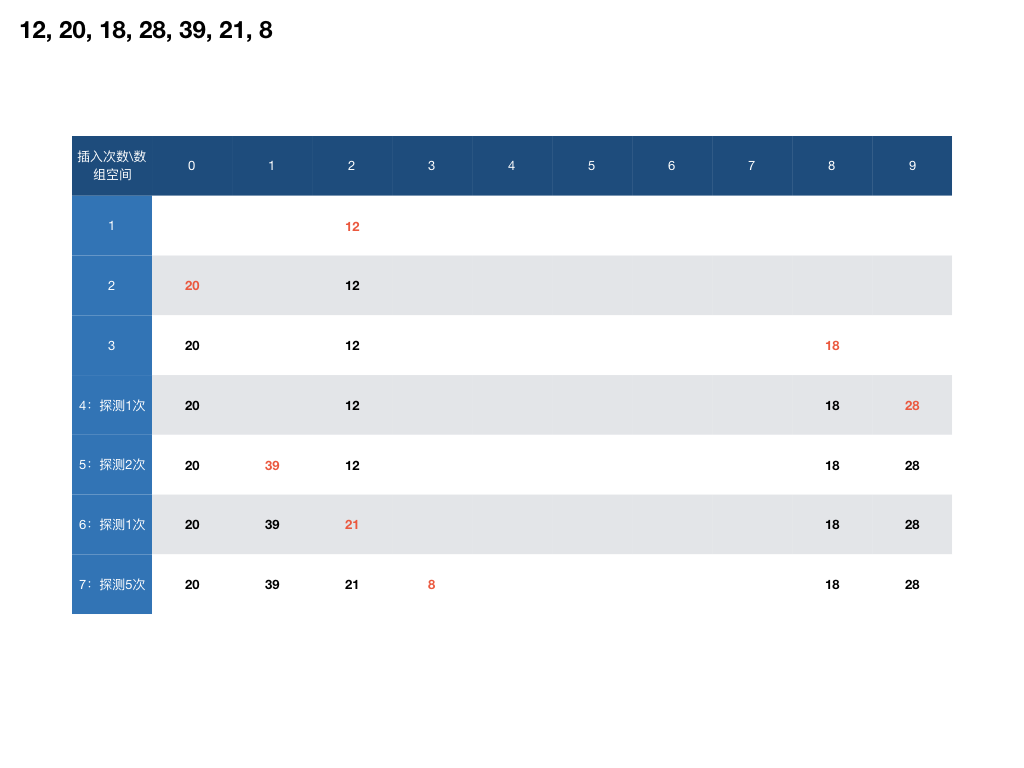
闭哈希遇到不同关键字处于同一位置的情况,会确定下一个可能存储的位置,其中最简单的一种是线性探测,当哈希函数计算出的位置存放了别的数据时,依次往后寻找。搜索时往往设定一些限定条件,例如探测次数超过表长就返回失败结果。
示例
大小为10的哈希表,哈希函数h(k)=k%10,依次插入数据 12, 20, 18,28,39,21,8 。
开哈希( Open Hashing )
由于使用了链表的形式存储数据,那么遇到哈希函数的结果已经被占的情况,只需要向链表追加一个结点。如果搜索的数据不存在,搜索时需要遍历结果位置链表上的每一个结点才能确认。
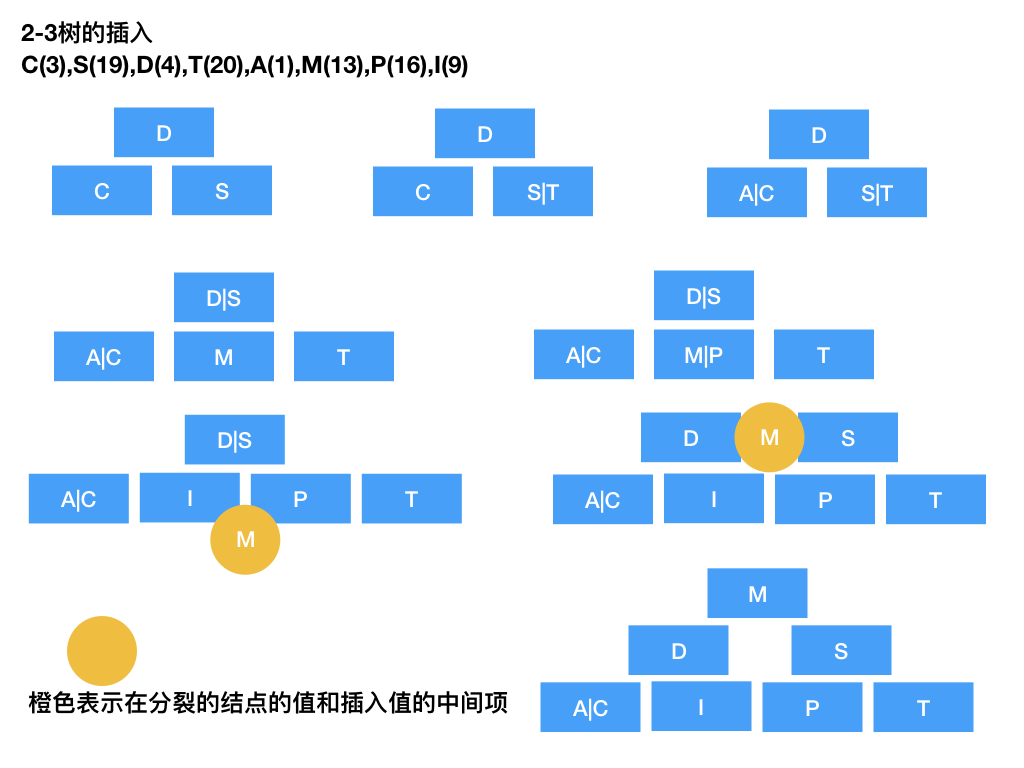
2-3树
2-3树意味着中间节点总是有2-3个孩子结点,所有叶子结点处于同一深度。这是一种自平衡的树。2-3树的结点最多可以存储两个数据,存储一个数据的中间节点有两个孩子,存储两个数据的中间结点有三个孩子。
有两个孩子结点时,父亲结点的值大于等于第一个孩子节点,小于第二个孩子结点,有三个孩子节点时,父亲结点的两个值也应该夹在第一、二个结点和第二、三个结点之间。
插入与删除
2-3树的插入自底向上,但需要先自顶向下找到合适的插入位置,如果那个位置没有满插入过程结束,如果满了,需要分裂(两个结点变三个结点,三个结点的情况分裂父亲结点,参与分裂的结点与插入项的中间项上移,如此递归),分裂可能会使树的高度升高。删除值可能会影响下级结点,需要触发分裂的反过程。插入与删除的具体实现不作介绍。
深度优先与广度优先
图的遍历分为深度优先(Depth First Search)与广度优先(Breadth First Search),从字面意思可以看出:
深度优先会先沿着顶点连接的某个顶点访问,当一个顶点所有的邻居(顶点连接的顶点)都被访问过,访问会回退到上一个顶点,继续寻找没有访问过的顶点,直至返回开始的顶点。
而广度优先则在访问完一个顶点的所有邻居后再访问邻居的邻居,如果所有邻居都被访问过,访问也会回退到上一个顶点。
最短路径长度与最小代价生成树
迪杰斯特拉算法(Dijkstra’s algorithm):单源最短路径
迪杰斯特拉算法帮助我们确定一个点到图中所有点的距离,它进行以下几个步骤(我们用D(A,P)表示数组中存储的A点到图上任意一点P的距离,用A-P表示A直接到P的路径长度):
- 建立一个数组D存储出发点A到所有其他点的距离,初始值设为无限大(一般用特殊值表示,如-1)。
- 将A到所有邻居的距离更新(更新为A-P)。
- 根据数组D,选择到A距离最短的点B(也是图中离A最近的点,只可能是直与A直接相连的点),对其设置标记,以其为出发点,更新其所有邻居到A的距离(比较D(A,P)与A-B-P,只有比数组中的记录更小才更新)。
- 根据数组D,选择到A距离最短并且没有标记过的点C(也是图中离A第二近的点,既可能与A直接相连,也可能与B相连),对其设置标记,以其为出发点,更新其所有邻居到A的距离(比较D(A,P)与D(A,C)+(C-P),只有比数组中的记录更小才更新)。
- 根据数组D,选择到A距离最短并且没有标记过的点D(也是图中离A第三近的点,既可能与A直接相连,也可能与B或C相连),对其设置标记,以其为出发点,更新其所有邻居到A的距离(比较D(A,P)与D(A,D)+(D-P),只有比数组中的记录更小才更新)。
- 根据数组D,选择到A距离最短并且没有标记过的点E(也是图中离A第四近的点),对其设置标记,以其为出发点,更新其所有邻居到A的距离(比较D(A,P)与D(A,E)+(E-P),只有比数组中的记录更小才更新)。
- 递归地选择、更新,我们会得到离A第n近的点,直至得到所有点离A的最短路径。
该算法中数组D可以是一个小顶堆,这样的改进使迪杰斯特拉算法在稀疏图中的复杂度降低(Theta约等于VlogV)。
Floyd算法:所有点对最短路径
虽然也可以重复使用迪杰斯特拉算法,但Floyd算法的复杂度远小于那种方式。
K-路径:如果一条路径的中间顶点的标号都小于K,称这条路径为K路径。(1-路径包含0-路径,因此才会有下面的不等关系)
定义Dk(v,u)为v到u的最短k路径长度,W(v,u)为v到u的连边权重,d(v,u)为v到u的最短路径长度,有以下关系
W(v, u) =D0(v, u) >= D1(v, u) >= D2(v, u) >= … >= Dn(v, u) = d(v, u)
Dk和Dk+1的关系:当k不在路径上,Dk=Dk+1,当k处于路径上,满足Dk(v,k)=Dk+1(v,k)和Dk(k,u)=Dk+1(k,u),因此Dk+1等于Dk和Dk(v,k)+Dk(k,u)两者的较小值。
因此我们总可以根据Dk与Dk(v,k)+Dk(k,u)推断出Dk+1,这就是Floyd算法的核心。
具体实现
由于计算所有点对的最短距离,Floyd算法需要一个邻接矩阵来存储最短路径长度(替换掉图中存储的直接连边长度),D0等于直接连边的长度;比较Dk(v,0)+Dk(0,u)和D0,选择较小的,所有D0更新为D1;比较Dk(v,1)+Dk(1,u)和D1,选择较小的,所有D1更新为D2……直到Dn+1(图中共有n个顶点)。
Prim算法最小代价生成树
子图开始只包含一个顶点,一步步地向子图添加顶点和边,不过每次都在子图连接的点中寻找离这个子图最近的点。
Kruskal算法最小代价生成树
初始状态所有顶点都是独立子图,寻找连边权重最小且分别属于两个子图的顶点,将两个子图通过这条连边连接在一起,重复这个过程直到只有一个子图,既最小代价生成树。
拓扑排序
对流程图而言,完成一些任务总需要满足某些先决条件,如果把这些任何和先觉条件画成一个有向图,我们可以对其进行拓扑排序。
拓扑排序时先为每个点设置入度(即有多少个顶点指向这个顶点),只有入度为0的点才能被加入排序序列,从起点开始,每加入一个顶点都使该顶点邻居的入度-1,然后在入度为0的点中选择顶点,直到完成拓扑排序。拓扑排序的结果序列通常有很多种,这取决于选择哪些0入度的点先加入序列。