快速排序算法，即一种递归地讲数组按一定大小标准分成两组，小的一组在前，大的一组排在后的算法。
有关快速排序算法的文章和图解，网络上已经很多了，但阅读理解起来可能稍有困难，接下来我们将看到更容易理解的快速排序算法。
示例：以数组的首位作为基准（pivot），将小于ta的数置于ta的左边，大于ta的数在右边，左边只有1个元素，排序完成，而右边有4个数，那么把这4个数作为新的要排序的（抽象的）数组，重复上面的过程，最终基准所在的（抽象的）数组只有基准一个元素（如下图第二排的“2”），排序完成。
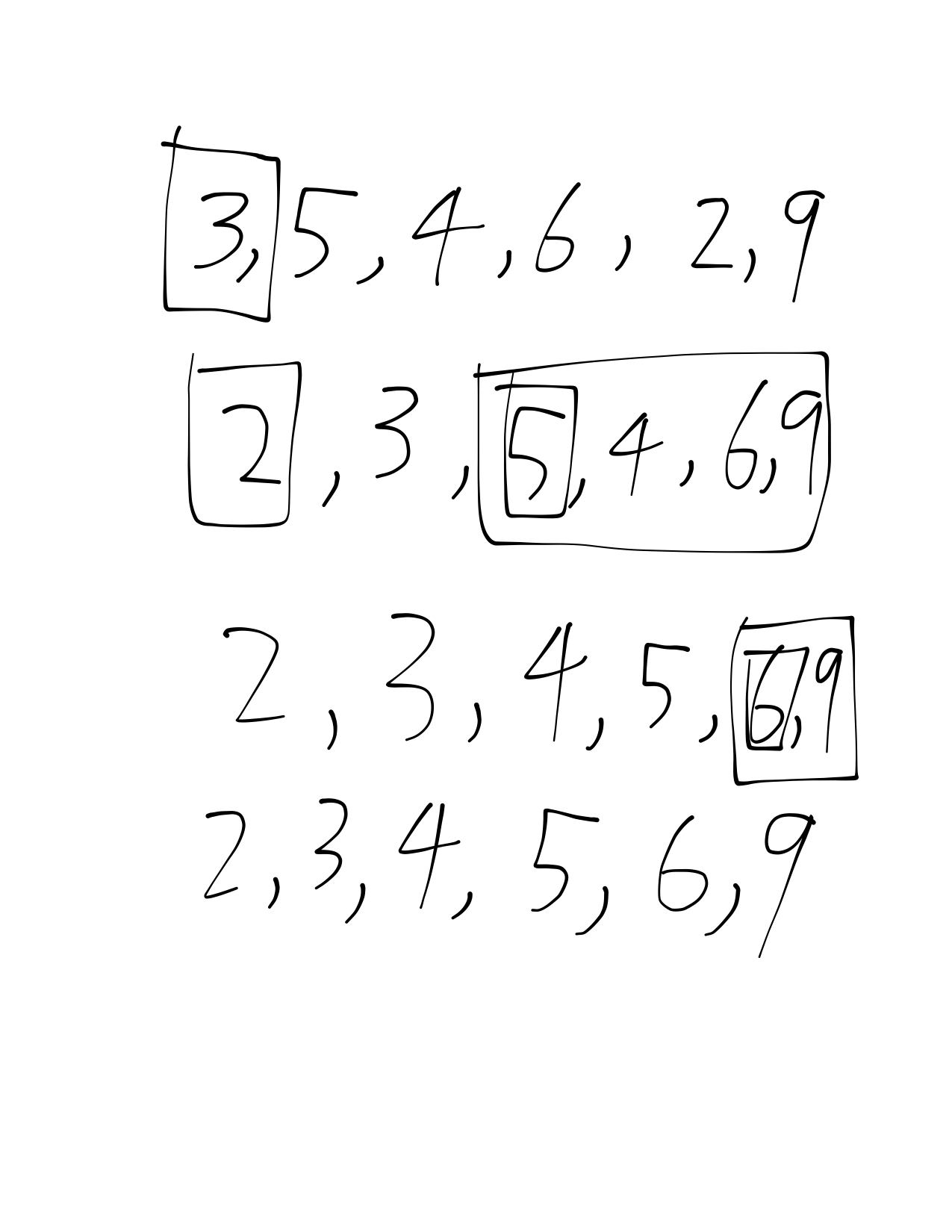
快速排序的复杂度
快排过程中需要移动元素的位置，很大程度上决定了时间复杂度。如果一个数组由大到小排列，而选取首位（最大数）为基准，则每一个元素都需要移动，而每一次移动的过程：对n个元素，考虑一般情况，分割一次数组（即小的排左边的过程）比较和交换元素的次数和n有关（虽然有的时候不用交换，但一定会比较）；而快排有一颗递归树，在数字比较随机，树比较均匀的情况下，树的高度近似logn，而树的每一层都有n个元素参与partition（数组分割成抽象数组后，多个抽象数组partition，因为partition的复杂度与n的一次方相关，在估测复杂度时，可以认为每一层都有n个元素参与一次partition），随机情况的复杂度即为n*logn。
最坏情况这棵树只沿着一颗子树延伸，树的高度为n，每一层仍有n个元素参与partition，复杂度为n*n。看一下数字从大到小排列的情况，例如100到1，首次partition会进行99次比较，最后一次partition进行1次比较，并且递归也会进行99次，从等差数列的公式也可以看出来它与n的平方相关。
复杂度的数学证明：
快速排序的代码（便于理解过程的版本，partition时移动数据，复杂度高）
#include <iostream>
using namespace std;
void QuickSort(int arr[],int start,int end){//递归的时候，start和end都相对于整个arr
if(start>=end){return;}
int temp=start;//保留start初始值
int pivot=arr[start];//以数组或分割后的抽象数组的第一个元素作为基准(pivot)
for(int i=start+1;i<=end;i++){//遍历arr[start]右边的元素
if(arr[i]<pivot){//当arr[i]比基准小
arr[start]=arr[i];//小的元素放到基准所在的位置
for(int j=i;j>start;j--){//遍历arr[start]到arr[i]，全体右移（arr[start]已经放了新的元素）
arr[j]=arr[j-1];//右移
}
arr[++start]=pivot;//由于start和i项交换，start+1项的值需要修正,完成交换后基准右移，所以start也要++
}
}//完成了一次左右分组（排序）
QuickSort(arr, temp, start-1);//对0号到start-1号元素排序，共有start个元素
QuickSort(arr, start+1, end);//对右边的元素排序
}
int main(int argc, const char * argv[]) {
int arr[]={3,4,2,7,5,8,6,1};//8个元素组成的的乱序数组
QuickSort(arr,0,7);//8个元素即0号到7号
for(int i=0;i<8;i++){
cout<<arr[i]<<endl;
}
return 0;
}
快速排序的代码（普通版本）
#include <iostream>
using namespace std;
int Partition(int arr[],int &start,int &end){
int pos=start;//(pos-start)用来记录小于等于arr[start]（基准）的数的个数，arr[start+1]到arr[pos]都小于基准
for(int i=start+1;i<=end;i++){//遍历基准以后的元素
if(arr[i]<arr[start]){//当某一项小于基准
if(arr[i]!=arr[++pos]){//如果任何一个大于基准的数后面所有元素中都没有小于x基准的数（即基准后的元素，前一部分全部小于基准，后一部分全部大于基准），则arr[i]==arr[pos]，不需要交换；否则需要交换
swap(arr[i], arr[pos]);
}
}
}
swap(arr[start], arr[pos]);//基准的位置开始没有移动，现在把基准的位置交换到小于基准的抽象数组的最右端，实现对数组的分割
return pos;
}
void QuickSort(int arr[],int start,int end){//递归的时候，start和end都相对于整个arr
if(start>=end){return;}//对应多种情况，pos可能等于start，pos-1为负，这种情况没有数小于基准，也不需要排序，对应start==end+1；pos等于start+1时，只有一个数比基准小，并且已经z位于基准左边，也不需要排序，对应start==end
int pos=Partition(arr, start, end);//对数组或抽象数组按基准排列，基准左边的数小于基准，右边大于基准
QuickSort(arr, start, pos-1);//对0号到start-1号元素排序，共有start个元素
QuickSort(arr, pos+1, end);//对右边的元素排序
}
int main(int argc, const char * argv[]) {
int arr[]={3,4,2,7,5,8,6,1};//8个元素组成的的乱序数组
QuickSort(arr,0,7);//8个元素即0号到7号
for(int i=0;i<8;i++){
cout<<arr[i]<<endl;
}
return 0;
}
两个指针的快速排序&&Partition的优化
待补充
参考资料：
1.《算法导论》第7章：快速排序
我的博客即将同步至腾讯云+社区，邀请大家一同入驻：https://cloud.tencent.com/developer/support-plan?invite_code=1q1xzkj9mydbq