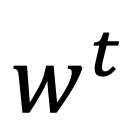矩阵
数字元素排列的矩形阵列
矩阵加法
大小相同的矩阵对相同位置的数字相加,自然也可以相减
矩阵乘法
矩阵和常数相乘
矩阵中每一个数都和这个常数相乘,这个意义上矩阵除以常数也没问题。不过从解方程的意义上讲,矩阵乘以常数之后还是一样的矩阵。
矩阵和矩阵相乘
当第一个矩阵的列数等于第二个矩阵的行数,他们可以相乘。乘法规则是,第一个矩阵第m行的元素与对应的第二个矩阵第n列的元素相乘,他们的结果再相加,得到了相乘后矩阵的第m行第n列元素(因此相乘的结果是一个m行n列的矩阵)。
从规则很快可以看出来,两个矩阵的位置是不能交换的,因此矩阵乘法不满足交换律;再结合矩阵加法的规则,模拟一下过程,可以看出来矩阵乘法满足分配律和结合律。矩阵乘法的规则可以从线性方程组的角度解释推导。
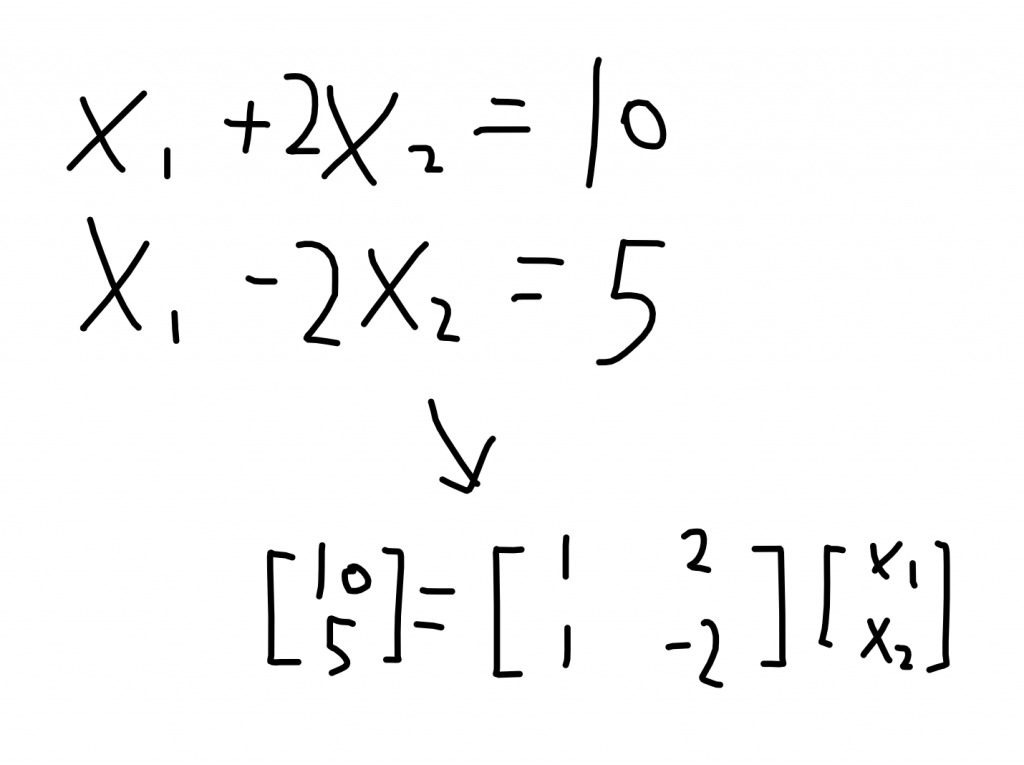
矩阵乘法与线性变换
我花了不少时间才明白上面是在说什么(丢
Rn是所有长度为n的行矢量,同样,Rm是所有长度为m的行矢量。现在Rn要变成Rm,实际上是Rn中的行矢量x能够映射到Rm中的某个行矢量。定义了f表示映射函数,用f(x)=Af*x表示经过矩阵的映射x得到长度为m的表示。
尽管是行矢量,但我们知道矩阵乘法要求第一个矩阵的列数要等于第二个矩阵的行数,因此算的时候竖着写,矢量x看作一个n*1的矩阵,能够得到一个m*1的矩阵,也就是映射后的矢量。通过矩阵,我们能够实现在维度不同的空间中映射矢量,但不一定可逆。
上图中二维平面的例子就是长度为2的矢量做变换,算是比较直观了。
内积与外积
向量的乘法产生内积与外积,其中外积是一个矩阵,内积是一个实数。
外积
m*1的列向量与1*n的行向量相乘,最终得到m*n矩阵,而这个矩阵上i行j列的值等于列向量第i行乘以行向量第j列。
内积
也叫点积,或者数量积,如果m=n,可以得到内积,高中数学就已经做过这样的计算。例如(a,b)*(c,d)=ac+bd
element-wise multiplication & matrix multiplication
前者相乘的规则是:对应位置上的元素分别相乘,因此两个矩阵大小应一致,numpy中用v*u表示。后者是矩阵乘法,用dot(v,u)。
矩阵转置
转置后的矩阵m行n列的元素是原来n行m列的元素,矩阵由n*m变为m*n。矩阵w转置的标记如图所示。